How can teachers help students find the beauty in math? There may be roadblocks already set up in math education -- students’ disposition toward math anxiety, and pressure to cover material quickly. Or maybe it has something to do with the curse of knowledge -- the gap between what experts know and non-experts don’t.
It’s easy for math professors to see the beauty in math, said New York University neuroscientist Pascal Wallisch, because they already have an obvious connection with it. “They perhaps had the luck to enjoy a positive math experience in school,” he said. “Or, frankly, from a cognitive neuroscience perspective, there is little doubt in my mind that they have quite a bit of a different brain than the average person who is trying to unlock the wonders of math, or just learn some math in order to get by.”
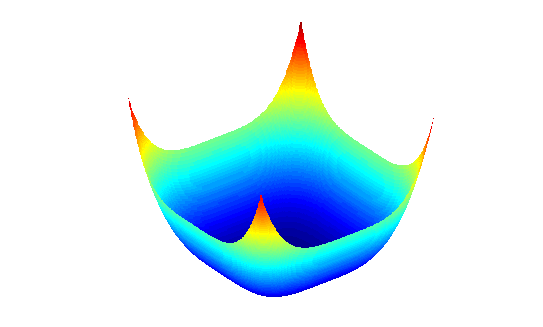
Wallisch said that as both a brain scientist and someone for whom math did not come easily, the key to mathematical beauty (and understanding) is visuals. “As primates, we are mostly visual creatures. A good amount of the cortex in primates (upwards of 30%) is dedicated to visual processing in one way or the other. Put differently, things that look interesting or appealing are bound to attract curiosity,” he said. Looking at a picture (or a movie or video) is the same thing as looking at an equation. But while it represents the same information, one method is inherently more appealing to our brains than the other.
According to Wallisch, mathematical imagery is what students are missing, and what causes confusion. He used the example of reading the words “Statue of Liberty,” and how it evokes an immediate image in the mind. But if a person couldn’t read, or had never heard of the Statue of Liberty, they would visualize only letters and words, not Lady Liberty holding her torch -- and the same goes for math novices. Since they have no experience, the mix of mathematical symbols on the page don’t mean much. “Mathematicians see equations by imagery built by long-term practice manipulating them,” he said. “The trick is to use software to visualize the equations so that those who don’t have the practice (or the unusual brain) can see the same.”

